どうも!RyeChemです!
今回の記事は【QC検定の数式一覧・早見表(前半Part)】になります!
今記事ではQC検定3級・2級の範囲を対象に、QC検定で頻出の数式を一覧に早見表としてまとめています。
数式を覚えるのだけがとにかく厄介なQC検定ですが、逆に言えば式さえ覚えてしまえばあとはそんなに難しくありません。
今回の記事では、前半Partということで『基本統計量』~『検定・推定』の分野までを収録しています。

- QC検定2級または3級の受験を考えている方
- 数式を覚えるのが苦手な方
- 数式の一覧表を見たい方
Contents
QC検定で扱う数式の一覧・早見表
今回の記事では基本統計量から『検定・推定』分野まで扱います!
その中で用いる数式の一覧表を以下に記します。基本的には全て覚えましょう。
| 基本統計量 | |
| 平均値 | \(\bar{x}=\frac{データの合計}{データの個数}=\frac{\displaystyle \sum_{i=1}^{n}x_i}{n}\) |
| メディアン | \(\tilde{x}\)=中央に位置する値(奇数)または 中央2つの値の平均値(偶数) |
| 範囲 | \(R=x(max)-x(min)\) |
| 平方和 | \(S=\sum(x_i-\bar{x})^2=\sum x_i^2-\frac{(\sum x_i)^2}{n}\) |
| 不偏分散 | \(V=\frac{S}{\phi}\) S:平方和, Φ(自由度)=n-1 |
| 標準偏差 | \(s=\sqrt{V}\) V:不偏分散 |
| 変動係数 | \(CV=\frac{s}{\bar{x}}\) |
| 工程能力指数 | ||
| Cp | \(Cp=\frac{規格上限-規格下限}{6×標準偏差}\) | |
| Cpk(規格上限) | \(Cpk=\frac{x_{max}-\bar{x}}{3×標準偏差}\) | Cpkはどちらか小さい値を採択 |
| Cpk(規格下限) | \(Cpk=\frac{\bar{x}-x_{min}}{3×標準偏差}\) | |
| 確率分布 | ||||
| 分布の種類 | 式 | 期待値 | 分散 | |
| 正規分布 | ガウス分布 | \(f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})\) | μ | σ2 |
| 標準化 | \(Z=\frac{x-\mu}{\sigma}\) | 0 | 12 | |
| 二項分布 | \(P(x)={}_n C_k \times p^x \times (1-p)^{n-x}\) | np | np(1-p) | |
| ポアソン分布 | \(P(x)=\frac{\mu^xe^{-\mu}}{x!}\) | λ | λ | |
| 検定・推定 | ||||
| 条件 | 統計検定量 | 上限 | 下限 | |
| 計量数平均 | 分散既知 | \(Z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) | \(\bar{x}+Z(\frac{\alpha}{2})\times\frac{\sigma}{\sqrt{n}}\) | \(\bar{x}-Z(\frac{\alpha}{2})\times\frac{\sigma}{\sqrt{n}}\) |
| 分散未知 | \(t=\frac{\bar{x}-\mu}{\frac{\sqrt{V}}{\sqrt{n}}}\) | \(\bar{x}+t(\phi、\alpha)\times\frac{\sqrt{V}}{\sqrt{n}}\) | \(\bar{x}-t(\phi、\alpha)\times\frac{\sqrt{V}}{\sqrt{n}}\) | |
| 計量数分散 | 集団1つ | \(\chi^2=\frac{S}{\sigma^2}\) | \(\chi^2(\phi、1-\frac{\alpha}{2})\) | \(\chi^2(\phi、\frac{\alpha}{2})\) |
| 集団2つ | \(F=\frac{V_B}{V_A}\) | \(F(\phi_B、\phi_A;\frac{\alpha}{2})\) | ||
| 計数値適合率 | 集団1つ | \(Z=\frac{p-P_0}{\sqrt{\frac{P_0(1-P_0)}{n}}}\) | \(p\pm Z(\frac{\alpha}{2})\times\frac{\sqrt{p(1-p)}}{\sqrt{n}}\) | |
| 集団2つ | \(Z=\frac{p_A-p_B}{\sqrt{\bar{p}(1-\bar{p})(\frac{1}{n_A}+\frac{1}{n_B})}}\) | \(p_A-p_B\pm Z(\frac{\alpha}{2})\sqrt{\frac{P_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}\) | ||
| 計数値適合数 | 集団1つ | \(Z=\frac{\hat{\lambda}-\lambda_0}{\sqrt{\frac{\lambda_0}{n}}}\) | \(\hat{\lambda}\pm Z(\frac{\alpha}{2})\times \frac{\sqrt{\hat{\lambda}}}{\sqrt{n}}\) | |
| 集団2つ | \(Z=\frac{\hat{\lambda_A}-\hat{\lambda_B}}{\sqrt{\hat{\lambda}\times (\frac{1}{n_A}+\frac{1}{n_B})}}\) | \(\hat{\lambda_A}-\hat{\lambda_B}\pm Z(\frac{\alpha}{2})\sqrt{\frac{\hat{\lambda_A}}{n_A}+\frac{\hat{\lambda_B}}{n_B}}\) | ||
基本統計量と工程能力指数
まず、基本的な統計量の算出と、実製造で定められた工程の評価手法に関して説明していきます。
基本統計量
母集団の中からサンプリングを行い、取り出した集団の各統計量を算出する式を以下にまとめます。
ここでは特に、平方和・不偏分散・標準偏差に関して、確実に覚えるようにしましょう。
| 平均値 | \(\bar{x}=\frac{データの合計}{データの個数}=\frac{\displaystyle \sum_{i=1}^{n}x_i}{n}\) |
| メディアン | \(\tilde{x}=中央に位置する値(奇数)または中央2つの値の平均値(偶数)\) |
| 範囲 | \(R=x(max)-x(min)\) |
| 平方和 | \(S=\sum(x_i-\bar{x})^2=\sum x_i^2-\frac{(\sum x_i)^2}{n}\) |
| 不偏分散 | \(V=\frac{S}{\phi}\) S:平方和, Φ(自由度)=n-1 |
| 標準偏差 | \(s=\sqrt{V}\) V:不偏分散 |
| 変動係数 | \(CV=\frac{s}{\bar{x}}\) |
平均値
平均値は数値の総和をサンプル数で除した値です。
データのほぼ中央に位置する値です。
“ほぼ”と記載したのは後述するメディアン値との区別のためです。
メディアン
測定値を大きさ順に並べた時の中央に位置する値です。
奇数の場合には中央に来る数字はただ1つに決まります。
ただ当然ですが、偶数の場合には数値が2つのため、その平均をメディアン値とします。
範囲R
一組の測定値の中の最大値と最小値の差です。
平方和S
個々の測定値と平均値との差の二乗の和で表される値です。
上記表中に記載の変形式の方がQC検定の計算問題ではよく利用されます。
ただ、文章説明では変形前の定義で登場することが多いので、結局どちらも覚えなければなりません。
不偏分散V
ばらつきの尺度を表す値であり、一般的には母分散の推定値として使用されます。
標準偏差
標準偏差sは不偏分散Vの平方根で表されます。
平方和・不偏分散と共に検定・推定問題等で頻出なので、確実に覚えましょう。
変動係数CV
標準偏差と平均値の比を変動係数といい、CVで表します。
それほど頻出ではありません。
工程能力指数
工程能力指数とは、定められた規格値の範囲内で製品を生産する能力の評価指標になります。
Cp≧1.67:十分すぎる
1.67>Cp≧1.33:十分満足できる
1.33>Cp≧1.0:及第点。十分な状態への改善を目指す
1.0>Cp≧0.67:不足しているため、要改善
Cp<0.67:完全に不足。原因究明と要処置
内容自体は頻出というほどでもありません。
ただ、算出式は簡単に覚えられるため、確実に記憶していきましょう。
両側規格Cpの場合
平均値を規格中央にコントロールできる場合に使用。
\(Cp=\frac{規格上限-規格下限}{6×標準偏差}\)
片側規格Cpkの場合
平均値が規格中央にコントロールできない場合に使用します。
つまり、グラフが正規分布様でなく、どちらかに裾が伸びたような非対称系を考慮した算出法になります。
上限・下限を求めた後、いずれかのCpkが小さい値を採択します。
①上限規格:\(Cpk=\frac{x_{max}-\bar{x}}{3×標準偏差}\)
②下限規格:\(Cpk=\frac{\bar{x}-x_{min}}{3×標準偏差}\)
確率分布
確率分布は正規分布を代表とする分布図であり、事象の確率を求めることが可能です。
これら3つの確率分布を用いた計算問題は頻出ですので、確実に覚えましょう。
正規分布
正規分布とは連続した左右対称な分布で、その確率密度関数f(x)は次の通りです。
ガウス分布とも呼ばれています。
\(f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})\)
正規分布は平均値=μと分散=σ^2によって定まる分布で、一般的に\(N(\mu、\sigma^2)\)と表します。
\(Z=\frac{x-\mu}{\sigma}\)
とおくと、xを\(N(0、1^2)\)に変換することができ、それを標準化、あるいは基準化と呼びます。
確率変数Zは\(期待値(平均値)=0、分散=1^2\)の正規分布に従い、このような正規分布\(N(0、1^2)\)を標準正規分布と呼びます。
この値と、正規分布表を用いることで事象の確率を算出できます。
逆に、事象の確率からZを算出し、標準偏差あるいは平均値を求めることもできます。
二項分布
\(P(x)={}_n C_k \times p^x \times (1-p)^{n-x}\)
で与えられる分布を二項分布と言います。

二項分布は\(B(n、p)\)で表されます。
また、その期待値は\(E(x)=np\), 標準偏差は\(\sigma(x)=\sqrt{np(1-p)}\)と表されます。
ポアソン分布
ポアソン分布は、まれにしか起こらない現象の出現度数分布にあてはまるといわれています。
母平均μが与えられたときに事象がx回出現する確率を表すポアソン分布の一般式は次の通り。
\(P(x)=\frac{\mu^xe^{-\mu}}{x!}\)
ポアソン分布の期待値は\(E(x)=\lambda\)、標準偏差は\(\sigma(x)=\sqrt{\lambda}\)と表されます。
期待値と分散が\(\lambda\)である、と覚えるといいでしょう。
期待値と分散の性質
- 確率変数に定数aを加えると期待値はaだけ増加、分散Vは変化しない。
- 確率定数に定数cを掛けると期待値はc倍に増加、分散Vはc^2倍に増加
- 2つの確率変数の和(差)の期待値は、おのおのの確率変数の和の期待値の和(差)に等しい。
- 2つの独立な確率変数の和の分散は、おのおのの確率変数の分散の和に等しい。
独立でない場合は、V(x)+V(y)+2Cov(x,y)と共分散項が現れる。
統計量の分布、検定統計量の算出
ここからは、実際のQC検定の問題で頻出の検定統計量の算出になります。

平均値の分布
母平均\(\mu\)、母分散\(\sigma^2\)の母集団から大きさnのサンプルをランダムに抽出したとき(母集団の分散が既知)、n個のサンプルの平均値xの平均値と分散
\(E(x)=\mu\)
\(V(x)=\frac{\sigma^2}{n}\)
\(Z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\)
このとき、Zを検定統計量と呼びます。
t分布
母分散が未知の集団から、サンプルをn個取り出した場合に検定統計量tは自由度\(\phi=n-1\)のt分布という分布で表されます。
このとき、検定統計量tは \(t=\frac{\bar{x}-\mu}{\frac{\sqrt{V}}{\sqrt{n}}}\) で表されます。
取り出したサンプル集団の不偏分散はVとします。
X2(カイの二乗)分布
\(N(\mu、\sigma^2)\)からn個のサンプルを取り、その平方和Sを\(\sigma^2\)で割ったものは自由度 \(\phi=n-1\) の \(\chi^2\)分布 で表されます。
\(\chi^2=\frac{S}{\sigma^2}\)
F分布
分散の等しい2つの正規分布から、それぞれランダムに取られたn1, n2のサンプルから得られた不偏分散を\(V_1、V_2\)とすると、
\(F=\frac{V_1}{V_2}\)となり、自由度 \(\phi_1=n_1-1、\phi_2=n_2-1\) のF分布に従います。
計量値の検定・推定
統計的検定とは、母集団からランダムにサンプリングした場合、その統計量を計算することで、母集団に関する各種の仮説に対して適否判定を行うものです。
例えば、ある反応で得られる固体の粒子径(μm)に着目しましょう。
この分布は母平均\(\mu\)=200.0で、母分散\(\sigma^2=20^2\)の正規分布をしているとします。
この実験において、撹拌速度を変更したところ、粒子径の平均が180.0になりました。
この時、撹拌速度変更による粒子径平均に与える影響が有意か否かを判定するなど、です。
証明したい仮説とは逆の仮説を帰無仮説\(H_0\)で表します。
帰無仮説とは反対に、本来証明したい仮説(対立仮説)を\(H_1\)で表します。
上記例の場合は、\(H_0=200.0\)で、\(H_1\neq200.0\)です。
判定により、平均が200.0から変化していると認められれば、「帰無仮説を棄却した」と言えます。
一方、変化が認められなかった場合「帰無仮説を棄却できなかった」と言え、帰無仮説を採択します。
このとき、有限の試行回数またはサンプル集団を基にした判定が真に母集団を反映しており、正しいとは言い切れません。
この場合に、仮説を捨てるか、捨てないかの判断をする小さな確率を危険率または有意水準と言い、\(\alpha\)で表します。

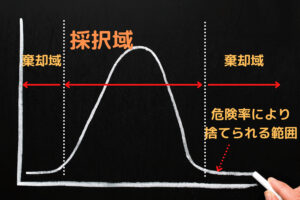
棄却域と棄却限界値
ある分布の有意水準、危険率により定められた棄却する範囲を棄却域と呼び、その限界点を棄却限界値と呼びます。
前述した各種分布の統計検定量と、対応する分布の有意水準によって定められる棄却限界値とを比較し、大小関係により仮説の適否判定を行います。
危険率と棄却限界値の対応表は正規分布、t分布、χ分布、F分布等が付属しているので、読み取るだけとなります。
平均値に関する検定
正規母集団からランダムに取られたn個のサンプルがある場合、母集団の平均値と試料平均値との間に差があるかどうかを検定します。
この場合に用いる検定統計量は2通りあります。
(1)母集団の分散\(\sigma^2\)が既知の場合:Z検定統計量
(2)母集団の分散\(\sigma^2\)が未知の場合:t検定統計量
上述の検定統計量の式に与えられた値を代入し、検定統計量を求めます。
また、有意水準と自由度から表を用いて、棄却限界値を得ます。
これら値を比較し、検定統計量>棄却限界値だった場合には、棄却域となりますので、帰無仮説を棄却します。
平均値に関する推定
推定とは、母集団から取り出したサンプルを統計的に処理することで、母集団の特性を知ることです。
真にある1つの値には決定することができませんが、十分に確からしい区間を推定することができます。
母分散が既知の場合
考えうる検定統計量の範囲は、棄却限界値(下限)≦検定統計量≦棄却限界値(上限)となります。
正規分布の棄却限界値は \(Z(\alpha)\)で表されます。
有意水準α=5%のとき、下限と上限に有意水準α=2.5%ずつの棄却域があると考え、以下のようになります。
\(-Z(\frac{\alpha}{2}) \le \frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}} \le Z(\frac{\alpha}{2})\)
上式を整理して、母平均μの推定値上限と下限は下記のようになります。
母平均μの上限は、 \(\bar{x}+Z(\frac{\alpha}{2})\times\frac{\sigma}{\sqrt{n}}\)
母平均μの下限は、 \(\bar{x}-Z(\frac{\alpha}{2})\times\frac{\sigma}{\sqrt{n}}\)
となります。
本推定区間の信頼度は1-αとなります。
母分散が未知の場合
上述の“母分散が既知”の場合と大きな差異はありませんが、母分散が未知のため母分散σは利用できません。
ここで、試料集団の不偏分散Vを考慮して、式を求めることとなります。
t分布の棄却限界値は、自由度Φと、有意水準αでt表から算出できます。
\(-t(\alpha) \le \frac{\bar{x}-\mu}{\frac{\sqrt{V}}{\sqrt{n}}} \le t(\alpha)\)
ここで、注意点があります。
t分布だけはt表に両側確率で有意水準αが記載されているため、\(\frac{α}{2}\)となりません。
※片側検定の場合には、上述の正規分布は\(Z(\alpha)\)、t分布の場合には\(t(2\alpha)\) となります。
よって、母平均μの上限は、\(\bar{x}+t(\phi、\alpha)\times\frac{\sqrt{V}}{\sqrt{n}}\)
母平均μの下限は、\(\bar{x}-t(\phi、\alpha)\times\frac{\sqrt{V}}{\sqrt{n}}\)
母分散に関する検定
平均とは変わり、母分散に関する検定ではχ2分布とF分布を使用します。
母分散の変化に関して
既に記載した、検定統計量 \(\chi^2=\frac{S}{\sigma_0}\) を利用します。
χ2分布を使用する注意点としては、分布が非対称系であることです。
つまり、平均値に関する検定で利用した正規分布やt分布のように、棄却限界値の上限と下限が同一の値とならないことです。
分散が大きくなったかを知る場合には棄却限界値 \(\chi^2(\phi、\frac{\alpha}{2})\)を用いて、検定統計量と比較します。
また、分散が小さくなったかを知る場合には棄却限界値 \(\chi^2(\phi、1-\frac{\alpha}{2})\)を用います。
自由度は\(\phi=n-1\)。
2つの母分散の違いに関して
2つの母分散の違いに関してはF分布を利用します。
例えば、装置Aと装置Bで得られるサンプルの分散を比較したい場合などですね。
検定統計量 \(F=\frac{V_B}{V_A}\) とおきます。
このとき、棄却限界値は \(F(\phi_B、\phi_A;\frac{\alpha}{2})\) です。
自由度は \(\phi_A=n_A-1、\phi_B=n_B-1\)となります。
母分散の推定
母分散の推定は非常に簡単に求めることができます。
点推定
点推定は、母分散を特定の1つの値に推定します。
\(V=\hat{\sigma}^2\)
区間推定
上限値=\(\frac{S}{\chi^2(\phi、1-\frac{\alpha}{2})}\)
下限値= \(\frac{S}{\chi^2(\phi、\frac{\alpha}{2})}\)
計数値の検定と推定
さきほどまでは計量値の検定と推定でした。
計量値とは量の単位があり、連続した値の事です。

ここでは、計数値の検定と推定を解説します。
計数値とは、個数を数えるような値です。

計数値の検定
計数価の検定や推定には二項分布とポアソン分布を用います。
ただ、QC検定レベルで出題される問題は、二項分布やポアソン分布が正規分布として近似される場合に限られます。
つまり、二項分布とポアソン分布で算出する検定統計量と、正規分布表の棄却限界値を比較することとなります。
二項分布では、\(np\ge5\) かつ\(n(1-p)\ge5\) であることが、正規分布として扱う条件となります。
ポアソン分布の場合には \(n\lambda\ge5\) です。
たまに、文字式部分か、数字部分が正規分布として扱う条件とは?という穴抜き問題で出題されます。
なので、条件に関しても覚えておくと良いでしょう。
不適合品“率”に関する検定と推定
不適合品率に関する検定と推定には二項分布を用います。
取り出した1つの集団の不適合品率と母集団の差異
P0=母不適合品率、p=試料中の不適合品率、x=不適合品数、n=試料数とおくと、
検定統計量 \(Z=\frac{p-P_0}{\sqrt{\frac{P_0(1-P_0)}{n}}}\) このとき、\(p=\frac{x}{n}\) となります。
仮説の判定には検定統計量と正規分布表の棄却限界値を使います。
帰無仮説を棄却:検定統計量≧棄却限界値
帰無仮説を棄却した場合には、取り出した試料から推定を行います。
点推定:\(\hat{P}=p=\frac{x}{n}\)
信頼率αの区間推定:\(p\pm Z(\frac{\alpha}{2})\times\frac{\sqrt{p(1-p)}}{\sqrt{n}}\)
取り出した2つの集団の不適合品率の差異
2つの集団をA、Bと置き、それぞれの所属を添え字で記載します。
検定統計量 \(Z=\frac{p_A-p_B}{\sqrt{\bar{p}(1-\bar{p})(\frac{1}{n_A}+\frac{1}{n_B})}}\)
ここで、\(\bar{p}=\frac{x_A+x_B}{n_A+n_B}\)
判定に関しては、正規分布として扱うので正規分布表の棄却限界値を用います。
母不適合率の推定は以下のようになります。
点推定:\(\hat{P_A}-\hat{P_B}=p_A-p_B\)
信頼率αの区間推定:\(p_A-p_B\pm Z(\frac{\alpha}{2})\sqrt{\frac{P_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}\)
不適合品数に関する検定
不適合品率に関しては、ポアソン分布を用います。
1つの集団の不適合品数に関して
母不適合数\(\lambda_0\)の集団から試料nを取って検査すると不適合品数がT個ある場合、試料の単位当たりの不適合数\(\hat{\lambda}\)を\(\lambda_0\)と比較します。
検定統計量 \(Z=\frac{\hat{\lambda}-\lambda_0}{\sqrt{\frac{\lambda_0}{n}}}\)
判定に関しては同様に正規分布表の棄却限界と比較します。
母不適合品数の推定は以下の通りです。
点推定:\(\hat{\lambda}=\frac{T}{n}\)
信頼率αの区間推定:\(\hat{\lambda}\pm Z(\frac{\alpha}{2})\times \frac{\sqrt{\hat{\lambda}}}{\sqrt{n}}\)
2つの不適合品数の違いに関して
2つの集団をA、Bと置き、それぞれの所属を添え字で記載します。
検定統計量:\(Z=\frac{\hat{\lambda_A}-\hat{\lambda_B}}{\sqrt{\hat{\lambda}\times (\frac{1}{n_A}+\frac{1}{n_B})}}\)
このとき、\(\hat{\lambda}=\frac{T_A+T_B}{n_A+n_B}\)
判定に関しては同様に正規分布表の棄却限界と比較します。
母不適合品数の推定は以下の通りです。
点推定:\(\hat{\lambda_A}-\hat{\lambda_B}\)
信頼率αの区間推定:\(\hat{\lambda_A}-\hat{\lambda_B}\pm Z(\frac{\alpha}{2})\sqrt{\frac{\hat{\lambda_A}}{n_A}+\frac{\hat{\lambda_B}}{n_B}}\)
今回の記事では、基本統計量~『検定・推定』分野までを紹介しました!